How to Traverse Back Up a Binary Search Tree

The recursive traversal algorithms work well for implementing tree-based ADT member functions, but if we are trying to hide the trees inside some ADT (e.g., using binary search trees to implement std::set), we may need to provide iterators for walking though the contents of the tree.

Iterators for tree-based data structures can be more complicated than those for linear structures.

For arrays (and vectors and deques and other array-like structures) and linked lists, a single pointer can implement an iterator:

Given the current position, it is easy to move forward to the next element.

For anything but a singly-linked list, we can also easily move backwards.

1 Iterating over Trees

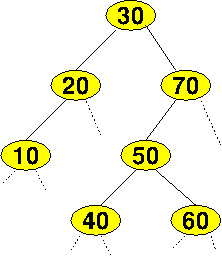
But look at this binary search tree, and suppose that you were implementing tree iterators as a single pointer. Let's see if we can "think" our way through the process of traversing this tree, one step at a time, without needing to keep a whole stack of unfinished recursive calls around.

We're going to try to visit the nodes in the same order we would process them during an "in-order" traversal, which, for a BST, means that we will visit the data in ascending order.

It's not immediately obvious what our data structure for storing our "current position" (i.e., an iterator) will be. We might suspect that a pointer to a tree node will be part or whole of that data structure, in only because that worked for us with iterators over linked lists. With that in mind, …

1.1 begin() and end()

Question: How would you implement begin()?

(Hint: which node is the first in an in-order traversal?)

Answer

We find the begin() position by starting from the root and working our way down, always taking left children, until we come to a node with no left child.

That doesn't sound so hard.

Careful, now.

Question: How would you implement end()?

Answer

Probably by returning a null pointer.

It's tempting to guess that you could do much the same as for begin(), this time seeking out the rightmost node. But that would leave you pointing to the last node in the tree, and end(), for any container, is supposed to denote the position after the last element in the container.

1.2 operator++

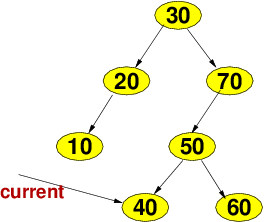
Now it gets trickier. Suppose you are still trying to implement iterators using a single pointer, you have one such pointer named current as shown in the figure.

Question: How would you implement ++current?

Answer

Well, we know that we should wind up at node 50. But how can we get there?

We can't, not with just a pointer to the node and all the nodes pointing only to their children. The only place you can go within this tree is down, and there is no "down" from our current position.

In a binary tree, to do operator++.

• We need to know not only where we are,

• but also how we got here.

One way is to do that is to implement the iterator as a stack of pointers containing the path to the current node. In essence, we would use the stack to simulate the activation stack during a recursive traversal.

But that's pretty clumsy. Iterators tend to get assigned (copied) a lot, and we'd really like that to be an $O(1)$ operation. Having to copy an entire stack of pointers just isn't very attractive.

2 Iterators using Parent Pointers

We can make the task of creating tree iterators much easier if we redesign the tree nodes to add pointers from each node to its parent.

These nodes are then used to implement a tree class, which, as usual, keeps track of the root of our tree in a data member.

A slightly subtle point here. The typedefs use the same data type for both the iterator and const_iterator types. That's because we really only want const-like behavior for thie ADT. If we provided a "true" non-const iterator, it would let reassign data in the tree:

which would very likely upset the internal ordering of data in the tree, making it useless for any future searches. So we are only going to provide a const-style iterator that allows us to look at data in the container but not change that data. That menas we only need one data type to implement both the iterator and const_iterator.

Later, when we use this tree to implement std::set and std::map, we'll see that this is precisely the behavior that they expect for their iterators.

2.1 Basic operations

Here's the basic declaration for an iterator to do in-order traversals.

                      class BstIterator     : public std::iterator<std::bidirectional_iterator_tag, Comparable> {   public:     BstIterator();          // comparison operators. just compare node pointers     bool operator== (const BstIterator& rhs) const;          bool operator!= (const BstIterator& rhs) const;          // dereference operator. return a reference to     // the value pointed to by nodePtr     const Comparable& operator* () const;          // preincrement. move forward to next larger value     BstIterator& operator++ ();          // postincrement     BstIterator operator++ (int);          // predecrement. move backward to largest value < current value     BstIterator  operator-- ();          // postdecrement     BstIterator  operator-- (int);        private:     friend class BinarySearchTree<Comparable>;          // nodePtr is the current location in the tree. we can move     // freely about the tree using left, right, and parent.     // tree is the address of the BinarySearchTree object associated     // with this iterator. it is used only to access the     // root pointer, which is needed for ++ and --     // when the iterator value is end()     const BinaryNode<Comparable> *nodePtr;     const BinarySearchTree<Comparable> *tree;          // used to construct an iterator return value from     // a node pointer     BstIterator (const BinaryNode<Comparable> *p,                  const BinarySearchTree<Comparable> *t);   };                  

The private section declares a pair of pointers. One points to the tree that we are walking through. The other points to the node denoting our current position within that tree.

2.2 begin() and end()

As discussed earlier, begin() works by finding the leftmost node in the tree:

          /**  * return an iterator pointing to the first item (inorder)  */ template <class Comparable> typename BinarySearchTree<Comparable>::const_iterator  inline BinarySearchTree<Comparable>::begin() const {   return BstIterator(findMin(root), this); }                  

And end() uses a null pointer.

          /**  * return an iterator pointing just past the end of  * the tree data  */ template <class Comparable> typename BinarySearchTree<Comparable>::const_iterator  inline BinarySearchTree<Comparable>::end() const {   return BstIterator(nullptr, this); }                  

Each of these functions calls upon a constructor for BstIterator :

                      class BstIterator {   public:     BstIterator();          // comparison operators. just compare node pointers     bool operator== (const BstIterator& rhs) const;          bool operator!= (const BstIterator& rhs) const;          // dereference operator. return a reference to     // the value pointed to by nodePtr     const Comparable& operator* () const;          // preincrement. move forward to next larger value     BstIterator& operator++ ();          // postincrement     BstIterator operator++ (int);          // predecrement. move backward to largest value < current value     BstIterator  operator-- ();          // postdecrement     BstIterator  operator-- (int);        private:            friend class BinarySearchTree<Comparable>;            const BinaryNode<Comparable> *nodePtr;     const BinarySearchTree<Comparable> *tree;            // used to construct an iterator return value from     // a node pointer     BstIterator (const BinaryNode<Comparable> *p,                  const BinarySearchTree<Comparable> *t);            };     ⋮            template <class Comparable> inline BinarySearchTree<Comparable>::BstIterator::BstIterator (const BinaryNode<Comparable> *p, const BinarySearchTree<Comparable> *t)   : nodePtr(p), tree(t) { }                  

That constructor is actually private within BstIterator, and so is not available to programmers to call directly. However, because the BstIterator class names BinarySearchTree as a friend, the BinarySearchTree code is allowed access to that private data and so can call that constructor from within its begin and end functions.

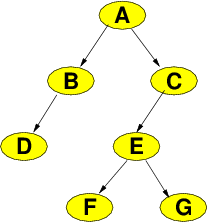Before trying to write the code for this iterator's operator++, let's try to figure out just what it should do.

Question: Suppose that we are currently at node E. What is the in-order successor (the node that comes next during an in-order traversal) of E?

**Answer**

G is the in-order successor of E. (If you answered F, remember that in an in-order traversal, we visit a node only after visiting all of its left descendents and before visiting any of its right descendents. Since we're at E, we must have already visited F.)

That example suggests that a node's in-order successor tends to be among its right descendents.

Let's explore that idea further.

Question: Suppose that we are currently at node A. What is the in-order successor (the node that comes next during an in-order traversal) of A?

**Answer**

F is the in-order successor of A.

If we are at A during an in-order traversal, we have already visited all of A's left descendents. So the answer has to be C or one of its descendents. It's tempting to pick C because it's only one step away from A. But, remember, during an in-order traversal, we visit a node only after visiting all of its left descendents and before visiting any of its right descendents. We have not yet visited C's left descendants. So have to run down from C to the left as far as we can go.

This suggests that, if a node has any right descendents, we should

• Take a step down to the right, then

• Run as far down to the left as we can.

You can see how this would take us from A to F. And, for that matter, it would take us from E to G as well. So both of our prior examples are satisfied.

But that "step to the right, then run left" procedure raises a new question. What happens if we are at a node with no right descendents?

Question: Suppose that we are currently at node C. What is the in-order successor of C?

**Answer**

C does not have an in-order successor. C is actually the final node in an in-order traversal. After C is only end().

OK, that's an interesting special case, but it doesn't make clear what should happen in the more general case where we have no right child.

Question: What is the in-order successor of F?

**Answer**

E is the in-order successor of F.

So, when we have no right child, we may need to move back up in the tree.

Question: What is the in-order successor of G?

**Answer**

C is the in-order successor of G.

Why did we move up two steps in the tree this time, when from F we only moved up one step? The answer lies in whether we moved back up over a left-child edge or a right-child edge.

If we move up over a right-child edge, we're returning to a node that has already had all of its descendents, left and right, visited. So we must have already visited this node as well, otherwise we would never have made it into its right descendants.

If we move up over a left-child edge, we're returning to a node that has already had all of its left descendents visited but none of its right descendents. That's the definition of when we want to visit a node during an in-order traversal, so it's time to visit this node.

So, if a node has no right child, we move up in the tree (following the parent pointers) until we move back over a left edge. Then we stop.

Notice that, applying this procedure to C, we would move up to A (right edge), then try to move up again to A's parent. But since A is the tree root, it's parent pointer will be null, which is our signal that C has no in-order successor.

​

2.3.1 Implementing operator++

To summarize,

• If the current node has a non-null right child,

  • Take a step down to the right

  • Then run down to the left as far as possible

• If the current node has a null right child,

  • move up the tree until we have moved over a left child link

With that in mind, the operator++ code should be easily :-) understood.

          // preincrement. move forward to next larger value template <class Comparable> typename BinarySearchTree<Comparable>::BstIterator& BinarySearchTree<Comparable>::BstIterator::operator++ () {   BinaryNode<Comparable> *p;      if (nodePtr == nullptr)     {       // ++ from end(). get the root of the tree       nodePtr = tree->root;              // error! ++ requested for an empty tree       if (nodePtr == nullptr)         throw UnderflowException { };              // move to the smallest value in the tree,       // which is the first node inorder       while (nodePtr->left != nullptr) {         nodePtr = nodePtr->left;       }     }   else     if (nodePtr->right != nullptr)       {         // successor is the farthest left node of         // right subtree         nodePtr = nodePtr->right;                  while (nodePtr->left != nullptr) {           nodePtr = nodePtr->left;         }       }     else       {         // have already processed the left subtree, and         // there is no right subtree. move up the tree,         // looking for a parent for which nodePtr is a left child,         // stopping if the parent becomes NULL. a non-NULL parent         // is the successor. if parent is NULL, the original node         // was the last node inorder, and its successor         // is the end of the list         p = nodePtr->parent;         while (p != nullptr && nodePtr == p->right)           {             nodePtr = p;             p = p->parent;           }                  // if we were previously at the right-most node in         // the tree, nodePtr = nullptr, and the iterator specifies         // the end of the list         nodePtr = p;       }      return *this; }                  

A similar process of analysis would eventually lead us to an implementation of operator–.

2.4 Working with Parents

There is, of course, a cost associated with this approach to iteration. We needed to add parent pointers to each node. That increases the storage overhead of the trees somewhat. It also means some modification to the code for building the trees. For example, here is our old code for inserting a data value into a BST:

          /**  * Internal method to insert into a subtree.  * x is the item to insert.  * t is the node that roots the subtree.  * Set the new root of the subtree.  */ template <typename Comparable> void BinarySearchTree::insert( const Comparable & x,  			       BinaryNode<Comparable> * & t) {   if( t == nullptr )     t = new BinaryNode{ x, nullptr, nullptr };   else if( x < t->element )     insert( x, t->left );   else if( t->element < x )     insert( x, t->right );   else     ;  // Duplicate; do nothing }                  

Here is the revised code, incorporating the parent pointers:

          /**  * Internal method to insert into a subtree.  * x is the item to insert.  * t is the node that roots the subtree.  * par is the parent node of t (null if t is the tree root)  * Set the new root of the subtree.  */ template <typename Comparable> void BinarySearchTree::insert( const Comparable & x,  			       BinaryNode<Comparable> * & t,  			       BinaryNode<Comparable> * par ) {   if( t == nullptr )     t = new BinaryNode<Comparable>{ x, nullptr, nullptr, par };   else if( x < t->element )     insert( x, t->left, t );   else if( t->element < x )     insert( x, t->right, t );   else     ;  // Duplicate; do nothing }                  

It's not terribly more complicated. Basically, we just have to remember that, if we are about to recursively visit a child of t, then we pass t as the parent pointer.

Another approach to supporting iteration is threading. Threading uses more complicated insert and remove algorithms to avoid the storage cost of addign the parent pointers.

Threaded trees replace all null right pointers by a thread (pointer) to that node's in-order successor.

need to add a boolean flag to each node to tell if the right pointer is a child or a thread

Can also thread the null left pointers to allow operator--

Follow the "right child" pointer.

If that pointer was not flagged as a thread, then descend as far to the left as possible.

operator++ never needs to move "up" in the tree (which, lacking a parent pointer, it can't do anyway).

The cost of this much simpler implementation of operator++ is a correspondingly more complicated implementation of the insert and remove functions, as these need to create and maintain the threads.

How to Traverse Back Up a Binary Search Tree

Source: https://www.cs.odu.edu/~zeil/cs361/latest/Public/treetraversal/index.html