Python How to Read String Vector to Array
In this lesson, nosotros will look at some slap-up tips and tricks to play with vectors, matrices and arrays using NumPy library in Python. This lesson is a very skillful starting point if you lot are getting started into Information Scientific discipline and need some introductory mathematical overview of these components and how nosotros can play with them using NumPy in code.
NumPy library allows u.s. to perform diverse operations which needs to exist done on information structures frequently used in Motorcar Learning and Data Science like vectors, matrices and arrays. Nosotros will only show nigh common operations with NumPy which are used in a lot of Machine Learning pipelines. Finally, delight annotation that NumPy is but a way to perform the operations, so, the mathematical operations we show are the principal focus of this lesson and non the NumPy bundle itself. Let's get started.
What is a Vector?
According to Google, a Vector is a quantity having direction every bit well as magnitude, especially as determining the position of one point in space relative to another.
Vectors are very important in Car Learning as they not just describe magnitude merely also the direction of the features. Nosotros tin create a vector in NumPy with following code snippet:
import numpy equally np
row_vector = np.array( [ ane,2,three ] )
print(row_vector)
In the to a higher place code snippet, nosotros created a row vector. We can also create a column vector as:
import numpy equally np
col_vector = np.array( [ [ 1 ],[ two ],[ 3 ] ] )
print(col_vector)
Making a Matrix
A matrix can exist simply understood as a two-dimensional array. Nosotros can make a matrix with NumPy by making a multi-dimensional array:
matrix = np.array( [ [ 1, 2, 3 ], [ iv, five, 6 ], [ 7, viii, ix ] ] )
print(matrix)
Although matrix is exactly similar to multi-dimensional assortment, the matrix information construction is non recommended due to 2 reasons:
- The array is the standard when it comes to the NumPy packet
- Almost of the operations with NumPy returns arrays and not a matrix
Using a Sparse Matrix
To remind, a thin matrix is the ane in which near of the items are null. Now, a common scenario in data processing and machine learning is processing matrices in which most of the elements are zero. For example, consider a matrix whose rows describe every video on Youtube and columns represents each registered user. Each value represents if the user has watched a video or not. Of course, majority of the values in this matrix will be zippo. The advantage with thin matrix is that it doesn't store the values which are zero. This results in a huge computational advantage and storage optimisation besides.
Allow'south create a spark matrix hither:
from scipy import thin
original_matrix = np.assortment( [ [ 1, 0, 3 ], [ 0, 0, 6 ], [ 7, 0, 0 ] ] )
sparse_matrix = sparse.csr_matrix(original_matrix)
impress(sparse_matrix)
To understand how the code works, we will look at the output here:
In the above code, nosotros used a NumPy's office to create a Compressed sparse row matrix where non-null elements are represented using the cypher-based indexes. There are diverse kinds of sparse matrix, like:
- Compressed thin cavalcade
- Listing of lists
- Dictionary of keys
We won't be diving into other sparse matrices hither simply know that each of their is utilise is specific and no ane can be termed as 'all-time'.
Applying Operations to all Vector elements
It is a common scenario when nosotros need to apply a common operation to multiple vector elements. This tin exist done by defining a lambda and and then vectorizing the same. Let'due south come across some code snippet for the same:
matrix = np.array( [
[ ane, 2, three ],
[ four, 5, 6 ],
[ 7, 8, ix ] ] )
mul_5 = lambda x: ten * v
vectorized_mul_5 = np.vectorize(mul_5)
vectorized_mul_5(matrix)
To understand how the code works, we will wait at the output here:
In the above lawmaking snippet, we used vectorize role which is part of the NumPy library, to transform a elementary lambda definition into a function which tin can process each and every element of the vector. It is of import to note that vectorize is just a loop over the elements and information technology has no effect on the functioning of the plan. NumPy besides allows broadcasting, which means that instead of the higher up complex code, we could have simply done:
And the effect would have been exactly the aforementioned. I wanted to testify the complex office offset, otherwise y'all would accept skipped the section!
Mean, Variance and Standard Deviation
With NumPy, information technology is piece of cake to perform operations related to descriptive statistics on vectors. Mean of a vector can be calculated as:
Variance of a vector tin be calculated as:
Standard deviation of a vector tin be calculated as:
The output of the above commands on the given matrix is given here:
Transposing a Matrix
Transposing is a very common operation which you will hear nigh whenever you are surrounded past matrices. Transposing is just a mode to swap columnar and row values of a matrix. Please note that a vector cannot be transposed every bit a vector is just a collection of values without those values being categorised into rows and columns. Please note that converting a row vector to a column vector is not transposing (based on the definitions of linear algebra, which is outside the telescopic of this lesson).
For now, we volition notice peace simply by transposing a matrix. Information technology is very unproblematic to access the transpose of a matrix with NumPy:
The output of the in a higher place control on the given matrix is given hither:
Aforementioned operation can be performed on a row vector to convert it to a column vector.
Flattening a Matrix
We can convert a matrix into a one-dimensional assortment if we wish to procedure its elements in a linear fashion. This can be done with the post-obit lawmaking snippet:
The output of the above command on the given matrix is given hither:
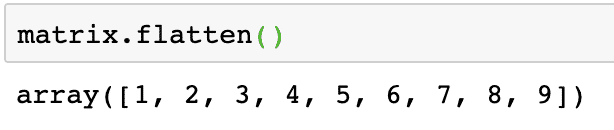
Note that the flatten matrix is a one-dimensional array, simply linear in fashion.
Calculating Eigenvalues and Eigenvectors
Eigenvectors are very commonly used in Machine Learning packages. So, when a linear transformation role is presented as a matrix, then Ten, Eigenvectors are the vectors that change only in calibration of the vector but not its direction. We can say that:
Here, X is the square matrix and γ contains the Eigenvalues. Likewise, v contains the Eigenvectors. With NumPy, it is easy to calculate Eigenvalues and Eigenvectors. Hither is the lawmaking snippet where we demonstrate the same:
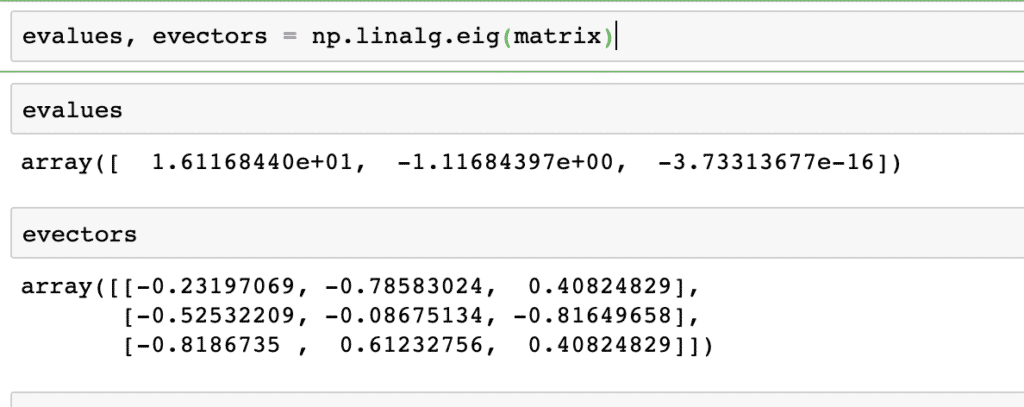
evalues, evectors = np.linalg.eig(matrix)
The output of the above command on the given matrix is given here:
Dot Products of Vectors
Dot Products of Vectors is a fashion of multiplying ii vectors. It tells you about how much of the vectors are in the same management, as opposed to the cross product which tells you the opposite, how little the vectors are in the aforementioned direction (called orthogonal). Nosotros tin can calculate the dot product of two vectors as given in the code snippet here:
a = np.array( [ three, 5, 6 ] )
b = np.array( [ 23, 15, 1 ] )
np.dot(a, b)
The output of the above command on the given arrays is given here:
Adding, Subtracting and Multiplying Matrices
Adding and Subtracting multiple matrices is quite straightforward functioning in matrices. In that location are two ways in which this tin can be done. Let's look at the lawmaking snippet to perform these operations. For the purpose of keeping this uncomplicated, we volition use the aforementioned matrix twice:
Next, two matrices can exist subtracted as:
np.decrease(matrix, matrix)
The output of the in a higher place command on the given matrix is given here:
As expected, each of the elements in the matrix is added/subtracted with the corresponding element. Multiplying a matrix is similar to finding the dot product equally we did earlier:
The above code will observe the true multiplication value of two matrices, given as:
The output of the higher up command on the given matrix is given here:
Conclusion
In this lesson, we went through a lot of mathematical operations related to Vectors, Matrices and Arrays which are commonly used Information processing, descriptive statistics and data science. This was a quick lesson roofing only the most common and most important sections of the wide variety of concepts but these operations should requite a very skillful thought about what all operations can exist performed while dealing with these data structures.
Please share your feedback freely about the lesson on Twitter with @linuxhint and @sbmaggarwal (that'due south me!).
About the author
I'one thousand a Java EE Engineer with near iv years of feel in edifice quality products. I have first-class problem-solving skills in Spring Kicking, Hibernate ORM, AWS, Git, Python and I am an emerging Data Scientist.
Source: https://linuxhint.com/python_vectors_matrices_arrays/
Post a Comment for "Python How to Read String Vector to Array"